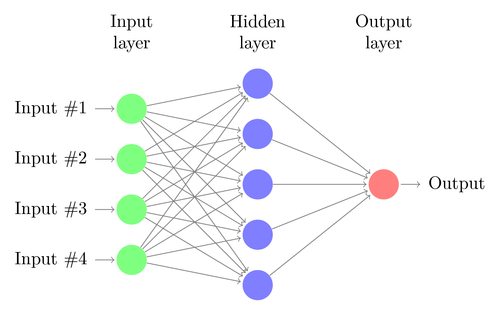
Shallow Neural Network
Shallow Neural Network (Regression)
Kenny Lov
A simple numpy implementation of a shallow (one layer) neural network for regression problems. Uses sigmoid activation function in the hidden layer. Backpropagation uses batch gradient descent to update parameters.
# import packages and data to test program
import numpy
from sklearn import datasets, preprocessing
X = datasets.load_boston().data
X = preprocessing.normalize(X)
y = datasets.load_boston().targetclass ShallowNet:
def __init__(self, params):
# collect desired size of layers
self.input_size = params['input_size']
self.hidden_size = params['hidden_size']
self.output_size = params['output_size']
# initialize weights
self.W1 = np.random.randn(self.hidden_size, self.input_size) # (hid_s, feature_s)
self.b1 = np.zeros((self.hidden_size,1)) # (hid_s, 1)
self.W2 = np.random.randn(self.output_size, self.hidden_size) # (out_s, hid_s)
self.b2 = np.zeros((self.output_size, 1)) # (out_s, 1)
def sigmoid(self, x): # sigmoid activation function
return 1/(1+np.exp(-x))
def sigmoid_p(self, x): # derivative of sigmoid function
return self.sigmoid(x) * (1-self.sigmoid(x))
def forward_prop(self, X):
self.Z1 = self.W1.dot(X.T) + self.b1 # (hid_s, feature_s) x (feature_s, sample_s)
self.A1 = self.sigmoid(self.Z1) # (hid_s, sample_s)
self.out = self.W2.dot(self.A1) + self.b2 #(out_size, hid_size) x (hid_s, sample_s)
def mse(self, y): # calculate cost
return np.sum((self.out-y)**2) / len(y)
def backward_prop(self, X, y, lr):
# calculate gradients with respect to loss
self.d_out = self.out - y
self.dW2 = (1/self.input_size) * self.d_out.dot(self.A1.T)
self.db2 = (1/self.input_size) * np.sum(self.d_out, axis=1, keepdims = True)
self.dZ1 = self.W2.T.dot(self.d_out) * self.sigmoid_p(self.Z1)
self.dW1 = (1/self.input_size) * self.dZ1.dot(X)
self.db1 = (1/self.input_size) * np.sum(self.dZ1, axis=1, keepdims= True)
# update weights using calculated gradients
self.W2 -= lr*self.dW2
self.b2 -= lr*self.db2
self.W1 -= lr*self.dW1
self.b1 -= lr*self.db1
def one_epoch(self, X, y, lr): # one epoch: forward and back prop
self.forward_prop(X)
self.backward_prop(X, y, lr)
def predict(self, X_pred):
Z1 = self.W1.dot(X_pred.T) + self.b1
A1 = self.sigmoid(Z1)
out = self.W2.dot(A1) + self.b2
return out
Testing my class on sample dataset (Scikit-learn's built in Boston housing data). The MSE decreases with every epoch.
# set parameters
epochs = 100 # number of epochs
lr = 0.001 # learning rate
hid_size = 20 # number of hidden nodes
net = ShallowNet({"input_size": X.shape[1], "hidden_size": hid_size, 'output_size': 1}) # instantiate class
for i in range(epochs):
net.one_epoch(X, y, lr)
print('Epoch: {} - MSE: {}'.format(i+1, net.mse(y)))Epoch: 1 - MSE: 793.0345556683468
Epoch: 2 - MSE: 362.87716141492405
Epoch: 3 - MSE: 194.2119238284208
Epoch: 4 - MSE: 122.08802074000201
Epoch: 5 - MSE: 94.23555429501137
Epoch: 6 - MSE: 84.39322553759308
Epoch: 7 - MSE: 81.02411345296193
Epoch: 8 - MSE: 79.80099187555813
Epoch: 9 - MSE: 79.25618599968593
Epoch: 10 - MSE: 78.9203150166109
Epoch: 11 - MSE: 78.64833191968954
Epoch: 12 - MSE: 78.39636763625683
Epoch: 13 - MSE: 78.15137771139001
Epoch: 14 - MSE: 77.90956951612256
Epoch: 15 - MSE: 77.66989707298116
Epoch: 16 - MSE: 77.43212186305499
Epoch: 17 - MSE: 77.19624025195081
Epoch: 18 - MSE: 76.96231591795106
Epoch: 19 - MSE: 76.73043103688902
Epoch: 20 - MSE: 76.50067179453062
Epoch: 21 - MSE: 76.27312362036895
Epoch: 22 - MSE: 76.0478691133489
Epoch: 23 - MSE: 75.82498672786402
Epoch: 24 - MSE: 75.60454973304854
Epoch: 25 - MSE: 75.38662534824276
Epoch: 26 - MSE: 75.17127405018766
Epoch: 27 - MSE: 74.95854906058393
Epoch: 28 - MSE: 74.74849601697166
Epoch: 29 - MSE: 74.54115282161862
Epoch: 30 - MSE: 74.33654965609004
Epoch: 31 - MSE: 74.13470914404212
Epoch: 32 - MSE: 73.93564664143233
Epoch: 33 - MSE: 73.73937063152908
Epoch: 34 - MSE: 73.5458832015912
Epoch: 35 - MSE: 73.35518057863823
Epoch: 36 - MSE: 73.16725370311546
Epoch: 37 - MSE: 72.98208882125353
Epoch: 38 - MSE: 72.7996680793263
Epoch: 39 - MSE: 72.6199701056339
Epoch: 40 - MSE: 72.4429705687215
Epoch: 41 - MSE: 72.2686427029599
Epoch: 42 - MSE: 72.09695779505923
Epoch: 43 - MSE: 71.92788562729466
Epoch: 44 - MSE: 71.76139487514861
Epoch: 45 - MSE: 71.59745345870111
Epoch: 46 - MSE: 71.43602884842372
Epoch: 47 - MSE: 71.27708832707148
Epoch: 48 - MSE: 71.12059921014018
Epoch: 49 - MSE: 70.96652902789744
Epoch: 50 - MSE: 70.81484567233433
Epoch: 51 - MSE: 70.66551751255605
Epoch: 52 - MSE: 70.51851348216624
Epoch: 53 - MSE: 70.3738031421297
Epoch: 54 - MSE: 70.2313567224509
Epoch: 55 - MSE: 70.09114514580064
Epoch: 56 - MSE: 69.95314003598374
Epoch: 57 - MSE: 69.81731371387934
Epoch: 58 - MSE: 69.68363918321678
Epoch: 59 - MSE: 69.55209010828325
Epoch: 60 - MSE: 69.42264078540158
Epoch: 61 - MSE: 69.29526610977273
Epoch: 62 - MSE: 69.16994153905102
Epoch: 63 - MSE: 69.04664305481371
Epoch: 64 - MSE: 68.925347122899
Epoch: 65 - MSE: 68.80603065341995
Epoch: 66 - MSE: 68.68867096111508
Epoch: 67 - MSE: 68.57324572656687
Epoch: 68 - MSE: 68.45973295870841
Epoch: 69 - MSE: 68.3481109589426
Epoch: 70 - MSE: 68.23835828711644
Epoch: 71 - MSE: 68.13045372952405
Epoch: 72 - MSE: 68.0243762690548
Epoch: 73 - MSE: 67.92010505755458
Epoch: 74 - MSE: 67.81761939042903
Epoch: 75 - MSE: 67.7168986834858
Epoch: 76 - MSE: 67.61792245198673
Epoch: 77 - MSE: 67.52067029186108
Epoch: 78 - MSE: 67.4251218630145
Epoch: 79 - MSE: 67.33125687465697
Epoch: 80 - MSE: 67.2390550725633
Epoch: 81 - MSE: 67.14849622817411
Epoch: 82 - MSE: 67.05956012944063
Epoch: 83 - MSE: 66.97222657331452
Epoch: 84 - MSE: 66.88647535978242
Epoch: 85 - MSE: 66.80228628734571
Epoch: 86 - MSE: 66.71963914984616
Epoch: 87 - MSE: 66.6385137345409
Epoch: 88 - MSE: 66.55888982133116
Epoch: 89 - MSE: 66.48074718305337
Epoch: 90 - MSE: 66.40406558674238
Epoch: 91 - MSE: 66.32882479578211
Epoch: 92 - MSE: 66.25500457286024
Epoch: 93 - MSE: 66.18258468364786
Epoch: 94 - MSE: 66.11154490112929
Epoch: 95 - MSE: 66.04186501050938
Epoch: 96 - MSE: 65.97352481463044
Epoch: 97 - MSE: 65.90650413983391
Epoch: 98 - MSE: 65.84078284220533
Epoch: 99 - MSE: 65.77634081414493
Epoch: 100 - MSE: 65.71315799120936